This is the second in a series of blog posts I’ve been working on during COVID isolation. It started with the idea of refreshing my systems design and software engineering skills, and grew in the making of it.
Part 1 describes ‘the problem’. A mathematics game designed to help children understand factors and limits which represents the board game Ludo.
In Part 2 I take you through the concepts of translating the rules and sequence of decisions made by the game into a visual model, and the implications for this when it came to converting it from a mental to an algorithmic model.
Get in touch on Twitter at @mr_al if you’d like to chat.

Before Hitting the Keys
I’d spent a bit of time reflecting on this problem. Having played a couple of games with Miss 11 at home, I sat down one night with a pencil and paper to work through the Marker journeys, and to identify what the key number patterns were.


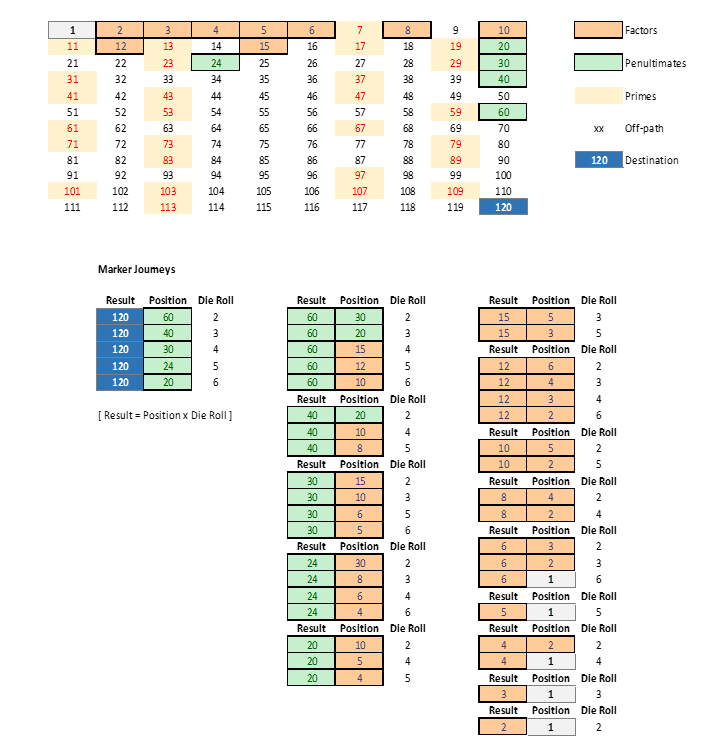
The table at the bottom is a neater representation of the result of where pieces will land, based on their current ‘position’ and the roll of the die.
The tables (and scribbles) above show this. The grid at the top of Figure 3 is the “playing board”. There are a finite number of Marker Positions that a ‘successful’ Marker will occupy as it traverses the board towards the destination of 120 (dark blue). There are also a known number of prime-number locations (above a value of 6, in red) that will never be landed on.
Accounting for the fact that a die roll of 1 results in a forfeited move, this means there are five ‘penultimate’ positions (light green) and nine ‘factor’ positions (orange) which represent the ‘well-worn path’ of successful Markers. If a Marker strays from the path – then they are doomed. They cannot re-join the successful path and will eventually be bumped or busted back to Position 1.
Why is this important? Because it gives the algorithm a fighting chance, rather than randomly picking pieces and hoping for the best.
The FASTEST possible journey is for a Marker to be moved resulting from any sequential roll consisting of one each of 4, 5 and 6 (moving it to position 4, 20 and 120 respectively… or a combination thereof). Of all the Markers available to move, the algorithm will look to prioritise one that is on the ‘fast track’ of factor and penultimate numbers.
Without this targeting, the game board may as well be hidden from view, with the Players each rolling their die and then calling out a blind guess as to what Marker to move. Maybe they’ll “count cards” and keep an image in their mind as to what Markers are where… but that is not the spirit in which the game was designed ?
Once the ideal Marker journeys had been identified, then came designing the functionality to have the algorithm make a choice based on the available evidence. This matured in the coding of it, and in the realisation that additional conditions – as captured in the description above – needed to be applied. Even a relatively simple game such as this one – used to teach primary school children mathematics basics – had logical layers like an onion.
Moving from Modelling to Design
I started with the design for the most basic Scenario Set – D. Moving a piece from ‘out of play’ to ‘in play’. This was relatively straight forward… until I realised that on the opening gambit that a Player may land on the Opposing Player’s Marker on only the second move of the game. (i.e. both rolled a ‘4’ on their first move… there is nowhere else they could go.)
So, the ‘detect clash’ became the next function designed. To do this, I needed a way of holding instances of both Player’s Markers so I could cycle through them and see if any were a hit. The first challenge to that was realising that there was an exception to the ‘occupy the same space’ rule. All Player’s Markers start at Position 1, and it is to that Position they return when bumped or busted. So, it had to ignore Markers on Position 1, and Markers that were ‘inactive’, having passed precisely through Position 120 on the way.
Battleships
The targeting of Opposition Player’s pieces in Scenario Set C came next. This was a variation on the logic used to detect clashes. Except, this time, it had to do some forecast calculations and then decide which piece to move. It was during the design for this method that I realised that I would not necessarily want to move a Marker ‘off the path’ or away from the fast-track, just to take out an Opponent. This was a lose-the-battle/win-the-war scenario. The logic behind choosing which Markers to target was tricky, and cost me most of my time in debugging, swearing and bourbon. I got there, eventually.
Priority Treatment
Design of the methods to target penultimate and factor Positions took a positive turn when I realised that the same logic could be applied to two different number sets. I wanted to give priority to the (green) penultimate numbers, so they became one set, and the factor numbers (orange) became the second. I applied them in that order. If a penultimate target was found, it was used. If not, the same searching logic was applied to factor numbers. I collectively referred to these as ‘magic numbers’, hence the naming in the code.
Are we there, yet?
Final trick was figuring out if it was game over. The original property design for Markers had a flag to indicate if it was active or not. I realised half way through coding that this was redundant, as was the property indicating who the owner was. Object orientation came to the rescue.
Basically – the owner was determined because the Marker was instantiated by a Player, and we would never reference a Marker without referencing the Player first. The second aspect was inelegant, but effective – once a Marker hit 120 exactly, the logic built around it would ignore any further moves involving it. The status flag was changed to a method – if you query this Marker and it’s Position is 120, it’s INACTIVE. Therefore… if you scan all a Player’s four markers and they each return INACTIVE… it’s game over.
Lovely. Time to start detailed design!
NEXT POST… Implementation design, class and method structure.

